The angle of a parallelogram
in 2D Drafting
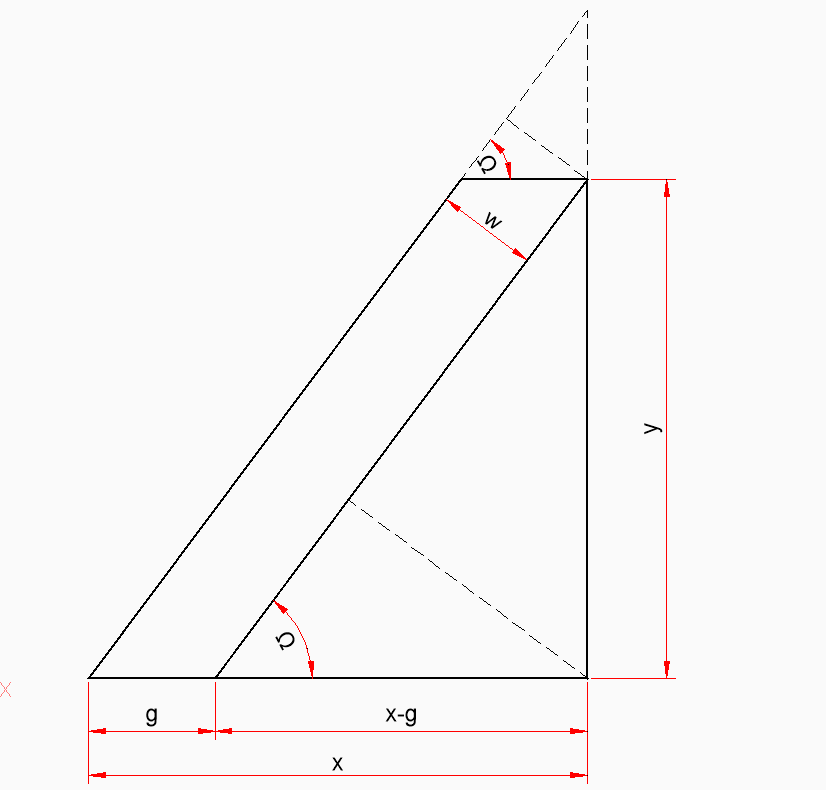
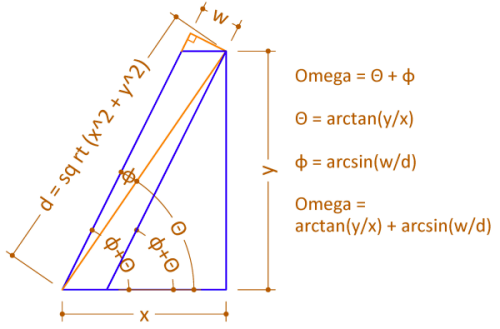
I'm trying to make a parametric drawing where struts find their correct angle. Given the attached diagram. Does anyone know how to mathematically find the angle from x,y and w ?
0
Comments
-
That's a tough one. I couldn't think of any way to draw that geometry given only lengths x, y, and w -- except by drawing a circle and then a line tangent to it. But I don't know how to write a mathematical expression for what the Tangent osnap does.
I do, however, think it would be pretty easy to use Lisp to draw the geometry and measure the angle Omega, if that helps. I don't know of any built-in way to measure an angle except DimAngular, but Stig Madsen's AngleM function does that.
(setq pt6 (inters pt2 pt3 pt1 pt5))
(command "AngleM" pt6 pt2 pt1) 0
0 -
You can use parallel and coincident 2D geometric constraints plus 2D dimensional constraints with parameters w,x, and y to fully define what you've drawn in the diagram. To solve for the angle Omega, the trigonometric identity sin(a-b)=sin(a)cos(b)-cos(a)sin(b) helps, or break it down as the sum of two angles.
Omega=arctan(y/x)+arcsin(w/d)
where d^2=x^2+y^2.
0 -
Shouldn't that be w/e?ScottS said:.... Omega=arctan(y/x)+arcsin(w/d)
where d^2=x^2+y^2.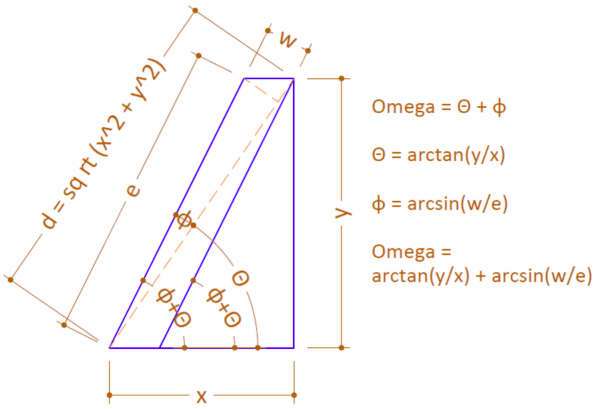 0
0 -
-
Good work, Igxavier. I could only check it as far as x sin Ω - y cos Ω = w. I didn't know how to solve for Ω, and couldn't even figure out how to use WolframAlpha to do it for me. But up to that point it looks good, and I assume the solution you got from them is correct.lgxavier said: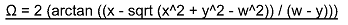
 0
0 -
Hi Anthony, I did some tests with numerical values and it seems OK.
In WolframAlpha, normally type the expression and indicate the variable to be evaluated. For example:
xsinø-ycosø=w, solve ø (and press 0
0 -
Hi Anthony, I did some tests with numerical values and it seems OK.
In WolframAlpha, normally type the expression and indicate the variable to be evaluated. For example:
xsinø-ycosø=w, solve ø ( and press = ).0 -
Yes, I see. Thank you. That's very useful. Though when I paste it in that way (xsinø-ycosø=w, solve ø), without the spaces, I get a very different answer.0
-
Well, I tested it now with and without spaces and, indifferent, same results for me. But the important thing is that it worked!0
-
Thanks Igxavier.
That is invaluable.
But now I'm going to be spending (and already have spent quite a few) hours trying to figure out why it is so. 0
0 -
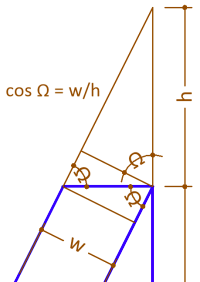
No. In the dashed right triangle with hypotenuse e in your diagram, the length opposite angle phi is close to (for small phi) but not quite w.Anthony Apostolaros said:
phi = arcsin(w/d)0 -
ScottS, your result for omega is correct and is much simpler. Congratulations!0
-
Yes, I see it now -- w is perpendicular to the blue lines, not to d. So d is the hypotenuse for angle phi.
 0
0