Angle between two 3D lines

VGonsalves

Hi

I am actually working with 3dPolylines and need to figure out the angle between two segements of this pline. Have been looking around for answers but have not found any.

Any suggestions on how to LISP this

Thanks

Tim_M

If you set up a UCS with:

the origin at the intersection

and the X axis along first segment

and the Y axis along the other segment

You should be able to then convert each of the points from WCS to UCS using the trans function

and then calculate the angles for each of the points using the angle function

and then calculate the difference

and then convert the result back to degrees

You should have the answer.

ALANH

Like Tim_M 3 answers, in XY plane, in a plane vert1- vert2 (think Z) and in a 3 point plane.

Which one do you want ?

VGonsalves

Hi Tim,

I actually tried that approach but seem to get a false result everytime. Maybe I have stuff something up

(acet-ucs-set (list p2 p1 p3)) (setq tp1 (trans p1 1 0) tp2 (trans p2 1 0) tp3 (trans p3 1 0) rBAng (/ (atof (angtos (- pi pi (- (angle tp2 tp1) (angle tp2 tp3))) 0 4)) 2))

This is what I have so far. Example would be - Draw any 3Dpolyline and use its points

Hi AlanH

Not sure I understand the question completely. I guess if you demonstrate achieving the three then maybe the penny will drop.

Thanks

Virgil

Hello.

One way of working could be to make a selection and get the points (vertices) that bound the two segments of the 3D polyline.

(vlax-curve-getClosestPointTo), (vlax-curve-getParamAtPoint), and (vlax-curve-getPointAtParam) could be useful here.

Once the four points have been obtained, they could be used to construct two vectors.
With vectors, the direction is an important factor.
For this case, the direction could be given by the sequence of points in the 3D polyline definition.

If you want the angle between the selected segments, then one of the vectors needs to be revrsed.
Otherwise, the angle will be calculated between a segment and the extension of the other one.

At this stage, the problem is to find the angle between two vectors in 3D.
Below is a link to an article that explains the procedure.
I picked this randomly from a search over Internet.
https://www.wikihow.com/Find-the-Angle-Between-Two-Vectors

Its_Alive

Using the geometry classes, getting an angle has two options, Using a reference vector, range [0, 2 x Pi], without is [0, Pi]

Consider:

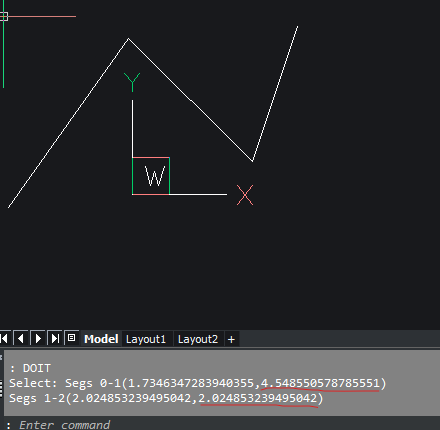
import traceback
from pyrx_imp import Rx, Ge, Gs, Db, Ap, Ed

def PyRxCmd_doit():
    try:
        res = Ed.Editor.entSel("\nSelect: ", Db.Polyline3d.desc())
        pl = Db.Polyline3d(res[1])
        composite = pl.getAcGeCurve()
        segs = [Ge.LineSeg3d.cast(s) for s in composite.getCurveList()]
        normal = Ge.Vector3d.kZAxis
        
        for i in range(1, len(segs)):
            lv = segs[i - 1].direction()
            rv = segs[i].direction()

            print("Segs {}-{} ({},{})".format(
                    i - 1, i, lv.angleTo(rv), lv.angleTo(rv, normal)))

    except Exception as err:
        traceback.print_exception(err)

VGonsalves

Hi Its_Alive,

Do you have LISP code for this? I am assuming the above is C code………… Maybe.

Thanks

Its_Alive

https://forum.bricsys.com/discussion/comment/53733#Comment_53733

It’s not available to lisp. I was just trying to illustrate the difficulty if the segments are not on the same plane.

The sample is Python scripting, from this project,

https://github.com/CEXT-Dan/PyRx

Tim_M

https://forum.bricsys.com/discussion/comment/53725#Comment_53725

Hi,

It looks like you are using the trans function wrong…

it should be (trans pt from to), where 0 is WCS and 1 is UCS…

so in your code - it should be (trans p1 0 1)  not (trans p1 1 0)  - and repeat for each point…

try those changes and see if it works…

Tim_M

Also….
If one of the segments is set to the X Axis (which should equate to an angle of 0.0 radians)

You should only have to check the angle of the other segment to get the angle between the segments.

ALANH

Have you looked at UCS 3 then Plan and can use DIM Ang.

Tom Foster

I was waiting for someone to say that! (my belief, not having time to test it myself)

VGonsalves

Sorry all, just got back to this issue. Tim_M I will try your suggestion. AlanH I get what you are saying but how do I capture the resultant value from that dimension. I am not interested in drawing dimensions I just need the angle for the next step

ALANH

The dim result is like any other Cad object has properties, so can read the angle , then delete the dim. Use (entget (entlast) ) do you know about DXf codes ? So get angle hint 42.

VGonsalves

Thank you all for your time. I have figured the best way forward for myself, "Law of cosines"

So, for anyone looking to do the same in the future, here is what I have

;https://en.wikipedia.org/wiki/Law_of_cosines

(setq a (distance p1 p2) b (distance p2 p3) c (distance p3 p1) rBAng (/ (rtod (acos (/ (- (+ (* a a) (* b b)) (* c c)) (* 2 a b)))) 2))

rBAng is the bisector angle value so if you simply need the angle ignore the /2

Bye now