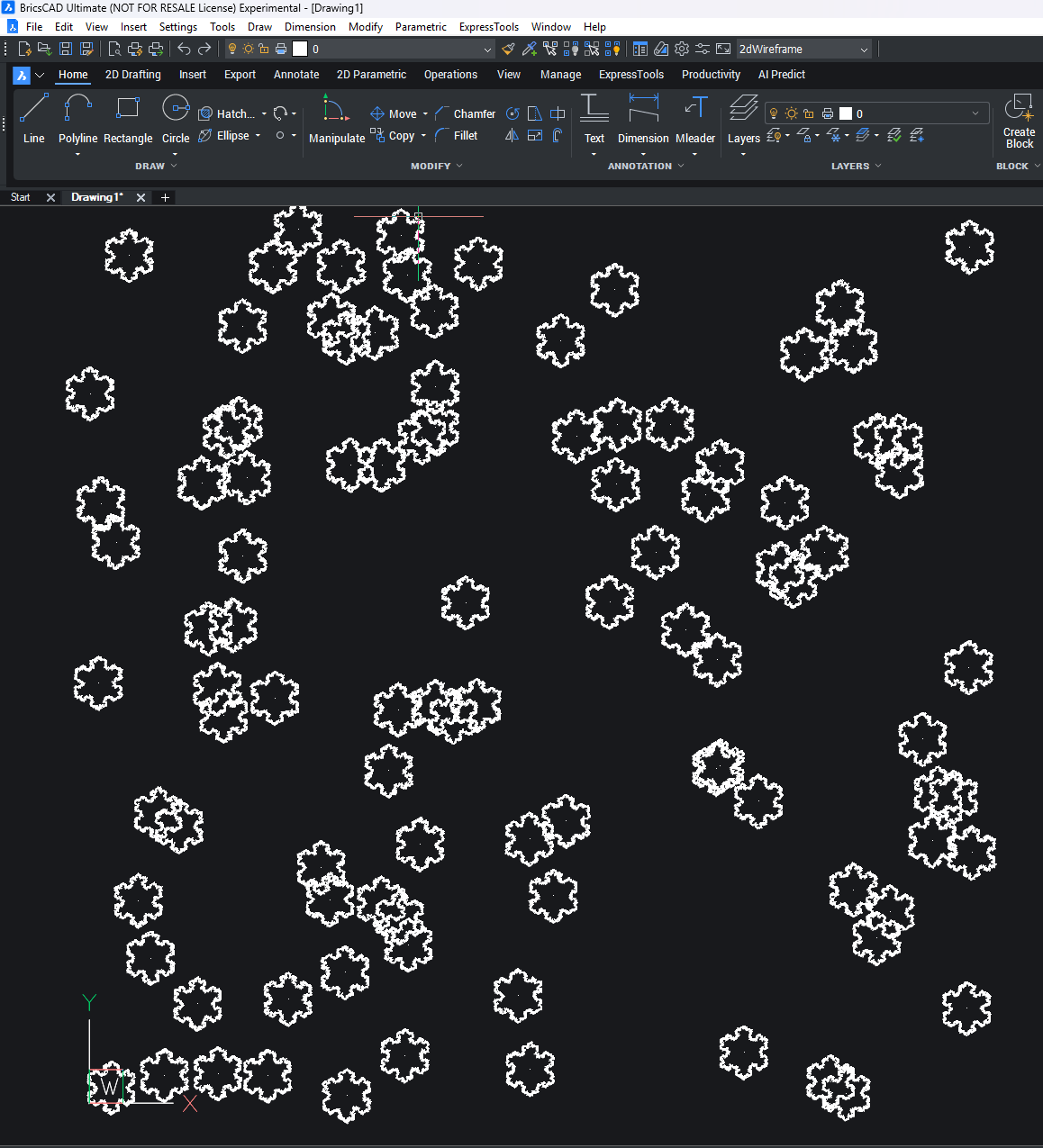
Random snowflake generator in Python for BricsCAD V26.

Its_Alive
Its_Alive
in Programming and customization

Illustrates PyRx, Python wrappers around BRX , Db.OverrulableEntity, an entity designed for overruling, Using Gi.DrawableOverrule to overrule the graphics of an object 

import traceback
import math
import random

from pyrx import Ap, Db, Ed, Ge, Gi
from typing import Tuple

class OrDrawOverrule(Gi.DrawableOverrule):
    def __init__(self) -> None:
        Gi.DrawableOverrule.__init__(self)

    # override
    def isApplicable(self, subject) -> bool:
        return True

    # override
    def worldDraw(self, subject, wd) -> bool:
        try:
            flag = self.baseWorldDraw(subject, wd)
            ore = Db.OverrulableEntity.cast(subject)
            geo: Gi.Geometry = wd.geometry()
            mat = Ge.Matrix3d.translation(ore.position() - Ge.Point3d.kOrigin)
            geo.pushModelTransform(mat)
            pnts = ore.points()
            for idx in range(1, len(pnts)):
                geo.polyline([pnts[idx - 1], pnts[idx]])
            geo.popModelTransform()
        except Exception as err:
            traceback.print_exception(err)
        finally:
            return flag

overrulableEntityDraw = None

def generate_single_3d_point(
    x_min: float, x_max: float, y_min: float, y_max: float, z_min: float, z_max: float
) -> Tuple[float, float, float]:
    """
    Generates a single random 3D point (x, y, z) within the defined cuboid limits.

    Args:
        x_min, x_max: Minimum and maximum bounds for the X-coordinate.
        y_min, y_max: Minimum and maximum bounds for the Y-coordinate.
        z_min, z_max: Minimum and maximum bounds for the Z-coordinate.

    Returns:
        A tuple representing the single point (x, y, z).
    """

    # Generate random coordinates for each axis
    x = random.uniform(x_min, x_max)
    y = random.uniform(y_min, y_max)
    z = random.uniform(z_min, z_max)

    return (x, y, z)


def generate_snowflake_edges(iterations: int, side_length: float = 100.0) -> list:
    """
    Generates the edges of a random-variant Koch snowflake fractal.

    Args:
        iterations: The number of recursive steps (fractal depth).
                    Higher value means more complex edges.
        side_length: The length of the initial hexagon's sides.

    Returns:
        A list of tuples, where each tuple represents an edge ((x1, y1), (x2, y2)).
    """

    # --- 1. Initial Edges (Setup for 6-fold symmetry) ---
    # A snowflake starts with a hexagon shape (6 edges).
    # We calculate the vertices of a hexagon centered at (0, 0).
    edges = []
    # Start angle: -pi/2 (to have a flat side at the top/bottom)
    start_angle = -math.pi / 2.0

    # Calculate initial six vertices
    for i in range(6):
        angle = start_angle + i * (math.pi / 3.0)  # 60 degrees * i

        # Calculate the coordinates of the start point of the current edge
        # We start the hexagon at the 6th point and iterate back for simplicity
        x1 = side_length * math.cos(angle - math.pi / 3.0)
        y1 = side_length * math.sin(angle - math.pi / 3.0)

        # Calculate the coordinates of the end point of the current edge
        x2 = side_length * math.cos(angle)
        y2 = side_length * math.sin(angle)

        # Add the initial edge: ((x_start, y_start), (x_end, y_end))
        edges.append(((x1, y1), (x2, y2)))

    # --- 2. Fractal Iteration ---
    # The Koch iteration breaks one line into four smaller lines.
    # We introduce a random variation to make it look unique.

    #

    for _ in range(iterations):
        new_edges = []
        for (x1, y1), (x2, y2) in edges:

            # 1. Calculate the vector of the current edge (v)
            vx = x2 - x1
            vy = y2 - y1

            # 2. Calculate the intermediate points for the 4 new segments

            # Point A (1/3 of the way along the segment)
            ax = x1 + vx / 3.0
            ay = y1 + vy / 3.0

            # Point B (2/3 of the way along the segment)
            bx = x1 + 2.0 * vx / 3.0
            by = y1 + 2.0 * vy / 3.0

            # Point C (The tip of the new triangle)
            # This is rotated 60 degrees (pi/3 radians) from the vector at point A.
            # Rotation matrix: (vx', vy') = (vx*cos(a) - vy*sin(a), vx*sin(a) + vy*cos(a))

            # We use cos(60) = 0.5 and sin(60) = sqrt(3)/2
            cos_60 = 0.5
            sin_60 = math.sqrt(3) / 2.0

            # Rotate the middle segment (1/3 of the full vector) by 60 degrees (outward)
            tip_vx = (vx / 3.0) * cos_60 - (vy / 3.0) * sin_60
            tip_vy = (vx / 3.0) * sin_60 + (vy / 3.0) * cos_60

            # C is A plus the rotated vector
            cx = ax + tip_vx
            cy = ay + tip_vy

            # --- Random Variation (The "Snowflake" part) ---
            # Add a small, random deviation to the tip point C to break the perfect fractal
            # and give each snowflake a unique appearance.
            RANDOM_FACTOR = 0.05  # Adjust this value for more or less randomness
            cx += random.uniform(-RANDOM_FACTOR * side_length, RANDOM_FACTOR * side_length)
            cy += random.uniform(-RANDOM_FACTOR * side_length, RANDOM_FACTOR * side_length)

            # 3. Create the 4 new edges
            new_edges.append(((x1, y1), (ax, ay)))  # 1st segment
            new_edges.append(((ax, ay), (cx, cy)))  # 2nd segment (to the tip)
            new_edges.append(((cx, cy), (bx, by)))  # 3rd segment (from the tip)
            new_edges.append(((bx, by), (x2, y2)))  # 4th segment

        edges = new_edges

    return edges


def gen_snowFlakes(num: int):
    snowFlakes = []
    for i in range(num):
        pnts = []
        ent = Db.OverrulableEntity()
        snowflake_edges = generate_snowflake_edges(iterations=4, side_length=150)
        for s, e in snowflake_edges:
            pnts.append(Ge.Point3d(s[0], s[1], 0.0))
            pnts.append(Ge.Point3d(e[0], e[1], 0.0))
        ent.setPoints(pnts)

        x, y, z = generate_single_3d_point(
            x_min=0.0, x_max=5000.0, y_min=0.0, y_max=5000.0, z_min=0.0, z_max=5000.0
        )
        ent.setPosition(Ge.Point3d(x, y, z))
        snowFlakes.append(ent)
    return snowFlakes


def OnDblClk(ent: Db.OverrulableEntity, pnt: Ge.Point3d):
    print("\nOMG it's a flake {},{}".format(ent.isA().name(), pnt))


@Ap.Command()
def startOverrule():
    global overrulableEntityDraw
    if overrulableEntityDraw is not None:
        return
    overrulableEntityDraw = OrDrawOverrule()
    overrulableEntityDraw.addOverrule(Db.OverrulableEntity.desc(), overrulableEntityDraw)
    overrulableEntityDraw.setIsOverruling(True)

    # register double click
    Db.OverrulableEntity.registerOnDoubleClick(OnDblClk)


@Ap.Command()
def letitsnow() -> None:
    try:
        db = Db.curDb()
        flakes = gen_snowFlakes(100)
        db.addToModelspace(flakes)
    except Exception as err:
        traceback.print_exception(err)
sn1.png

Comments